Al margen un sello con el Escudo Nacional, que dice: Estados Unidos Mexicanos.- ECONOMÍA.- Secretaría de Economía.- Dirección General de Normas.
ALFONSO GUATI ROJO SÁNCHEZ, Director General de Normas y Presidente del Comité Consultivo Nacional de Normalización de la Secretaría de Economía (CCONNSE), con fundamento en los Arts. 34, fraccs. XIII y XXXIII de la Ley Orgánica de la Administración Pública Federal; 5, 39 fracción V, 40 fraccs. IV, VIII y XVIII, 47 fracción I de la Ley Federal sobre Metrología y Normalización, 33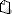 de su Reglamento y 36
de su Reglamento y 36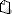 fraccs. I, IX y X del Reglamento Interior de esta Secretaría, expide para consulta pública el PROY-NOM-008-SE-2020, “SISTEMA GENERAL DE UNIDADES DE MEDIDA” (CANCELARÁ AL PROY-NOM-008-SCFI-2017
fraccs. I, IX y X del Reglamento Interior de esta Secretaría, expide para consulta pública el PROY-NOM-008-SE-2020, “SISTEMA GENERAL DE UNIDADES DE MEDIDA” (CANCELARÁ AL PROY-NOM-008-SCFI-2017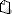 PUBLICADO EN EL DOF EL 24 DE JULIO DE 2018 Y A LA NOM-008-SCFI-2002
PUBLICADO EN EL DOF EL 24 DE JULIO DE 2018 Y A LA NOM-008-SCFI-2002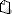 ), a efecto de que dentro de los siguientes 60 días naturales los interesados presenten sus comentarios ante el CCONNSE, ubicado en calle Pachuca número 189, colonia Condesa, demarcación territorial Cuauhtémoc, Código Postal 06140, Ciudad de México, teléfono 57 29 61 00, extensiones 13241 y 13238, o bien a los correos electrónicos rebeca.rodriguez@economia.gob.mx y cielo.beltran@economia.gob.mx, para que en los términos de la Ley de la materia se consideren en el seno del Comité que lo propuso. SINEC-20200327124756008.
), a efecto de que dentro de los siguientes 60 días naturales los interesados presenten sus comentarios ante el CCONNSE, ubicado en calle Pachuca número 189, colonia Condesa, demarcación territorial Cuauhtémoc, Código Postal 06140, Ciudad de México, teléfono 57 29 61 00, extensiones 13241 y 13238, o bien a los correos electrónicos rebeca.rodriguez@economia.gob.mx y cielo.beltran@economia.gob.mx, para que en los términos de la Ley de la materia se consideren en el seno del Comité que lo propuso. SINEC-20200327124756008.
Ciudad México, a 17 de diciembre de 2020.- El Director General de Normas y Presidente del Comité Consultivo Nacional de Normalización de la Secretaría de Economía, Lic. Alfonso Guati Rojo Sánchez.- Rúbrica.
PROY-NOM-008-SE-2020, “SISTEMA GENERAL DE UNIDADES DE MEDIDA
(Cancela al PROY-NOM-008-SCFI-2017 y a la NOM-008-SCFI-2002
y a la NOM-008-SCFI-2002 )
)
0. Introducción
Este Proyecto de NOM tiene como propósito describir el Sistema General de Unidades de Medida que establece la Ley Federal sobre Metrología y Normalización vigente en su artículo 5, como el único legal y de uso obligatorio en el país. Con ello se establece la forma de expresar los resultados de mediciones físicas y químicas que responde a las exigencias actuales de las actividades científicas, tecnológicas, educativas, industriales, comerciales u otras, al alcance de todos los sectores del país.
Este Proyecto de NOM tiene su origen principal en el documento Le Systéme international d’unités SI 2014 publicado por la Oficina Internacional de Pesas y Medidas (BIPM por sus siglas en francés), el cual incluye todas las resoluciones y acuerdos que, sobre el Sistema Internacional de Unidades (SI), ha tomado la Conferencia General de Pesas y Medidas (CGPM), en el ámbito del Tratado del Metro del cual México es signatario.
El Sistema General de Unidades de Medida (SGUM), objeto de este Proyecto de NOM, se integra con las unidades del Sistema Internacional de Unidades (SI) y con otras unidades de medida no comprendidas en el SI pero aceptadas para usarse con el mismo. Por ello, este Proyecto de NOM recoge las unidades de medida del SI incluyendo sus denominaciones, definiciones y símbolos, así como los prefijos y reglas de escritura para su utilización.
El SI es el primer sistema de unidades de medida coherente, esencialmente completo y armonizado internacionalmente, y está fundamentado en siete unidades de base que se han llevado a la práctica mediante los patrones de medida correspondientes. El SI facilita la estructuración de sus sistemas metrológicos a todos los niveles de exactitud en y entre las naciones que lo adopten.
El valor de una magnitud se expresa generalmente como el producto de un número por una unidad. La unidad no es más que un valor particular de la magnitud considerada, tomada como referencia, y el número es el cociente entre el valor de la magnitud considerada y la unidad. Para una magnitud concreta, se puede utilizar una amplia variedad de unidades. Por ejemplo, la velocidad v de una partícula puede expresarse como 25 metros por segundo o 90 kilómetros por hora, en donde metro por segundo y kilómetro por hora son unidades alternativas equivalentes para expresar el mismo valor de la magnitud velocidad. Sin embargo, debido a la importancia de contar con un conjunto de unidades bien definidas y de fácil acceso, que sean reconocidas universalmente para la multitud de medidas que requiere la compleja sociedad de hoy en día, las unidades deben elegirse de forma que sean accesibles a todo el mundo, constantes en el tiempo y el espacio, y fáciles de realizar con alta exactitud.
Conformar un sistema de unidades, tal como el Sistema Internacional de Unidades, el SI, requiere en primer lugar de un sistema de magnitudes, que incluya una serie de ecuaciones que definan las relaciones entre estas magnitudes. Estas ecuaciones son necesarias porque las relaciones entre las magnitudes determinan de manera similar las relaciones entre sus unidades. Es conveniente también elegir un reducido número de unidades, denominadas unidades de base, con la finalidad de que a partir de ellas se definan las unidades de todas las demás magnitudes, denominadas unidades derivadas, como producto de potencias de las unidades de base. De forma similar, las magnitudes correspondientes se denominan magnitudes de base y magnitudes derivadas, y las ecuaciones que expresan las magnitudes derivadas en función de las magnitudes de base se emplean para expresar las unidades derivadas en función de las unidades de base. Así en la lógica de desarrollo del tema, la elección de las magnitudes y de las ecuaciones que las relacionan precede a la elección de las unidades.
El SI es un sistema de unidades de medida coherente porque las unidades derivadas pueden expresarse en términos de productos de potencias de las unidades de base sin requerir ningún factor diferente de la unidad. Por ejemplo, la unidad derivada de la velocidad es el metro por segundo, que se expresa en términos de las unidades de base de longitud y tiempo como m·s-1. Otra unidad para la velocidad es km·h-1, la cual se expresa en términos de las unidades de base como 3.6 km·h-1 = 1 m·s-1; como hay entre ellas un factor diferente de 1, la unidad km·h-1 no es coherente con la unidad m·s-1. Debe notarse que el uso de múltiplos o submúltiplos de las unidades de base provocan la pérdida de la coherencia.
Por lo cual, este Proyecto de NOM contiene los requisitos para el uso de las unidades, símbolos y reglas de escritura de las unidades del SGUM que deben observarse al expresar resultados de medición en el país y contiene apéndices de naturaleza informativa acerca de otras unidades de medida.
1. Objetivo y campo de aplicación
Este Proyecto de NOM establece las definiciones, símbolos y reglas de escritura de las unidades del Sistema General de Unidades de Medida, para utilizarse en los ámbitos donde las cantidades se refieran a propiedades de cuerpos, fenómenos o sustancias de naturaleza física, química o biológica, independientemente de sus aplicaciones en los diferentes campos de la ciencia, la tecnología, la industria, la educación, la salud, el medio ambiente, el comercio u otros.
2. Referencias normativas
La siguiente Norma Mexicana, vigente o la que la sustituya, es indispensable para la aplicación del presente Proyecto de NOM. En tanto no exista NOM o Norma Mexicana correspondiente se podrá hacer referencia a Normas Internacionales, en los términos que establecen la Ley Federal sobre Metrología y Normalización y su Reglamento en lo conducente.
2.1 NMX-Z-055-IMNC-2009 Vocabulario Internacional de Metrología-Conceptos fundamentales y generales, y términos asociados (VIM), Declaratoria de Vigencia publicada en el DOF el 24 de diciembre de 2009.
2.2 Guía ISO/IEC 99: 2007 International vocabulary of metrology-Basic and general concepts and associated terms (VIM).
| Nota explicativa nacional
A continuación, se indica el grado de concordancia de la Norma Internacional señalada en las referencias normativas respecto a las normas:
| Norma Internacional | Norma | Grado de Concordancia |
| Guía ISO/IEC 99: 2007 | NMX-Z-055-IMNC-2009 | No equivalente (NEQ) |
 |
|
3. Términos y definiciones
Para la correcta aplicación de este Proyecto de NOM aplican las definiciones de la NMX-Z-055-IMNC-2009.
4. Generalidades
En la expresión de las medidas en los ámbitos donde éstas se refieran a propiedades de cuerpos, fenómenos o sustancias de naturaleza física, química o biológica, independientemente del campo de sus aplicaciones:
a) Deben usarse las unidades de medida de base del SGUM y sus símbolos según se muestran en el Capítulo 5 de este Proyecto de NOM.
b) Deben utilizarse los símbolos de las unidades de medida derivadas de acuerdo a lo indicado en el Capítulo 5 de este Proyecto de NOM.
c) Deben utilizarse los prefijos y las reglas de escritura de acuerdo a lo indicado en el Capítulo 6 de este Proyecto de NOM.
NOTA 1: El uso de las unidades de medida del SI en la expresión de resultados de medición supone que existe una relación de los valores de dichos resultados con las definiciones de las unidades del SI. Estas definiciones se llevan a la práctica mediante los valores de los correspondientes patrones nacionales de medida. Se dice entonces que los resultados de medición así expresados tienen la propiedad de trazabilidad metrológica.
5. Unidades de medida del SGUM. Magnitudes, definiciones y símbolos
5.1 Unidades de base
Las magnitudes y unidades de base del SGUM se muestran en la Tabla 1. La aplicación de los símbolos de las unidades SI de base es un requisito de este Proyecto de NOM.
Tabla 1-Magnitudes y unidades de base del SGUM, y símbolos de las unidades de base.
| Magnitudes de base | Unidades SI de base |
| Nombre | Nombre | Símbolo |
| longitud | metro | m |
| masa | kilogramo | kg |
| tiempo | segundo | s |
| corriente eléctrica | ampere | A |
| temperatura termodinámica | kelvin | K |
| cantidad de sustancia | mol | mol |
| intensidad luminosa | candela | cd |
La Tabla 2 contiene las definiciones de las unidades de base.
Tabla 2-Definiciones de las unidades de base.
| metro | es la longitud de la trayectoria recorrida en el vacío por la luz durante un lapso de 1/299 792 458 de segundo. |
| kilogramo | es igual a la masa del prototipo internacional del kilogramo |
| segundo | es la duración de 9 192 631 770 periodos de la radiación correspondiente a la transición entre los dos niveles hiperfinos del estado fundamental del átomo de cesio 133 |
| ampere | es la corriente eléctrica constante que, manteniéndose en dos conductores paralelos, rectilíneos, de longitud infinita, de sección circular despreciable y situados a una distancia de 1 metro uno del otro, en el vacío, produciría entre estos conductores una fuerza igual a 2 × 107 newton por metro de longitud. |
| kelvin | es la fracción 1/273.16 de la temperatura termodinámica del punto triple del agua. |
| mol * | es la cantidad de sustancia de un sistema que contiene tantas entidades elementales como átomos hay en 0.012 kilogramos de carbono 12. |
| candela | es la intensidad luminosa, en una dirección dada, de una fuente que emite una radiación monocromática de frecuencia 540 × 1012 hertz y cuya intensidad energética en dicha dirección de 1/683 watt por estereorradián. |
| * Cuando se emplee el mol, deben especificarse las entidades elementales, que pueden ser átomos, moléculas, iones, electrones u otras partículas o grupos especificados de tales partículas. |
5.2 Unidades derivadas
5.2.1 Generalidades
Las unidades derivadas se forman a partir de productos de potencias de unidades de base. Las unidades derivadas coherentes son productos de potencias de unidades de base en las que el único factor numérico que interviene es el 1. Las unidades de base y las unidades derivadas coherentes del SI forman un conjunto coherente, denominado conjunto de unidades SI coherentes.
El número de magnitudes utilizadas en la ciencia, la industria y otras actividades no tiene límite; por tanto, no es posible establecer una lista completa de magnitudes y unidades derivadas. Para unidades derivadas y unidades derivadas coherentes, expresadas en función de la unidad SI de base, puede consultarse la Tabla 3.
Tabla 3-Ejemplos de unidades SI derivadas coherentes expresadas a partir de las unidades SI de base.
| Magnitud derivada | Unidad SI derivada coherente |
| Nombre | Nombre | Símbolo |
| área, superficie | metro cuadrado | m2 |
| volumen | metro cúbico | m3 |
| velocidad | metro por segundo(a) | m·s–1 |
| aceleración | metro por segundo cuadrado | m·s–2 |
| número de onda | metro a la potencia menos uno | m–1 |
| densidad | kilogramo por metro cúbico | kg·m–3 |
| densidad superficial | kilogramo por metro cuadrado | kg·m–2 |
| volumen específico | metro cúbico por kilogramo | m3·kg–1 |
| densidad de corriente | ampere por metro cuadrado | A·m–2 |
| intensidad de campo magnético | ampere por metro | A·m–1 |
| concentración de cantidad de sustancia(b) | mol por metro cúbico | mol·m–3 |
| fracción de cantidad de sustancia | mol por mol | mol·mol–1 |
| fracción de masa | kilogramo por kilogramo | kg·kg–1 |
| concentración de masa | kilogramo por metro cúbico | kg·m–3 |
| luminancia | candela por metro cuadrado | cd·m–2 |
| índice de refracción(c) | uno | 1 |
| permeabilidad relativa(c) | uno | 1 |
| (a) Como es habitual en el país, en todos los casos el uso del término “por” indica una operación de división, y no de multiplicación. En las expresiones algebraicas se recomienda utilizar la notación exponencial y el signo “.” para indicar multiplicación.
(b) En el ámbito de la química clínica, esta magnitud se llama también concentración de sustancia.
(c) Son magnitudes adimensionales o magnitudes de dimensión uno. El símbolo “1” de la unidad (el número “uno”) se omite cuando se indica el valor de las magnitudes adimensionales. |
5.2.2 Unidades con nombres y símbolos especiales
Por conveniencia, ciertas unidades derivadas coherentes reciben nombres y símbolos especiales. Son en total veintidós y se describen en la Tabla 4. Estos nombres y símbolos especiales pueden utilizarse con los nombres y los símbolos de las unidades de base o derivadas para expresar las unidades de otras magnitudes derivadas. Algunos ejemplos de ello figuran en la Tabla 5. Los nombres y símbolos especiales son una forma compacta de expresar combinaciones de unidades de base de uso frecuente, pero en muchos casos sirven también para recordar la magnitud en cuestión. Los prefijos del SI pueden emplearse con cualquiera de los nombres y símbolos especiales, pero al hacerlo la unidad resultante no es más una unidad coherente.
La última columna de las Tablas 4 y 5 muestra la expresión de las unidades SI mencionadas en función de las unidades SI de base. No se muestran explícitamente los factores de la forma m0, kg0, etc., que son iguales a 1, (Aviso que da a conocer la autorización del Patrón Nacional de Rapidez de Ka en la Energía de 137Cs para Aplicaciones de Protección Radiológica, así como la cédula con descripción, magnitud, definición, unidad, alcance, incertidumbre, ubicación y medidas a las que provee trazabilidad, DOF 21/IX/2018 )
)
Tabla 4-Unidades SI derivadas coherentes con nombres y símbolos especiales.
Magnitud derivada | Unidad SI derivada coherente(a) |
Nombre | Símbolo | Expresión mediante otras unidades del SI | Expresión en unidades SI de base |
ángulo plano | radián(e) | rad | 1 (c) | mm–1 |
ángulo sólido | estereorradián
(e,f) | sr | 1 (c) | m2m–2 |
frecuencia | hertz(g) | Hz | (d) | s–1 |
fuerza | newton | N | (d) | mkgs–2 |
presión | pascal | Pa | N·m–2 | m–1kgs–2 |
energía, trabajo, cantidad de calor | joule | J | N m | m2kgs–2 |
potencia | watt | W | J·s–1 | m2kgs–3 |
carga eléctrica | coulomb | C | W/A–1 | sA |
tensión eléctrica, diferencia de potencial eléctrico | volt | V | WA–1 | m2kgs–3A–1 |
capacitancia | farad | F | CV–1 | m–2kg–1s4A2 |
resistencia eléctrica | ohm | O | VA–1 | m2kgs–3A–2 |
conductancia | siemens | S | AV–1 | m–2kg–1s3A2 |
flujo magnético | weber | Wb | Vs | m2kgs–2A–1 |
densidad de flujo magnético(j) | tesla | T | Wbm–2 | kgs–2A–1 |
inductancia | henry | H | WbA–1 | m2kgs–2A–2 |
temperatura Celsius | grado Celsius(h) | °C | (d) | K |
flujo luminoso | lumen | lm | cdsr | cd |
iluminancia | lux | lx | lmm–2 | cd m–2 |
actividad de radionucleido(i) | becquerel | Bq | (d) | s–1 |
dosis absorbida, energía específica (impartida), kerma | gray | Gy | Jkg–1 | m2s–2 |
dosis equivalente, dosis equivalente ambiental, dosis equivalente direccional y dosis equivalente personal | sievert | Sv | J/kg | m2s–2 |
actividad catalítica | katal | Kat (b) | (d) | s–1mol |
(a) Como es habitual en el país, en todos los casos el uso del término “por” indica una operación de división, y no de multiplicación. En las expresiones algebraicas se recomienda utilizar la notación exponencial y el signo “” para indicar multiplicación.
(b) En el ámbito de la química clínica, esta magnitud se llama también concentración de sustancia.
(c) Son magnitudes adimensionales o magnitudes de dimensión uno. El símbolo “1” de la unidad (el número “uno”) se omite cuando se indica el valor de las magnitudes adimensionales.
(d) Los prefijos SI pueden emplearse con cualquiera de los nombres y símbolos especiales, pero en este caso la unidad resultante no es una unidad coherente.
(e) El radián y el estereorradián son nombres especiales del número uno, que pueden usarse para proporcionar información respecto a la magnitud a que se refieren. En la práctica, los símbolos rad y sr se emplean donde sea apropiado, mientras que el símbolo de la unidad derivada “uno” no se menciona cuando se dan valores de magnitudes adimensionales.
(f) En fotometría se mantiene generalmente el nombre estereorradián y el símbolo sr en la expresión de las unidades.
(g) El hertz sólo se utiliza para los fenómenos periódicos y el becquerel para los procesos estocásticos relacionados con la actividad de un radionucleido.
(h) El grado Celsius es el nombre especial del kelvin empleado para expresar las temperaturas Celsius y es una unidad derivada. El grado Celsius y el kelvin tienen la misma magnitud, por lo que el valor numérico de una diferencia de temperatura o de un intervalo de temperatura es idéntico cuando se expresa en grados Celsius o en kelvin.
(i) La actividad de un radionucleido se llama algunas veces, de manera incorrecta, radioactividad.
(j) A la densidad de flujo magnético también se la conoce como inducción magnética. |
Tabla 5-Ejemplos de unidades SI derivadas coherentes cuyos nombres y símbolos contienen unidades SI derivadas coherentes con nombres y símbolos especiales.
| Magnitud | Unidad SI derivada coherente |
| Nombre | Símbolo | Expresión en unidades SI de base |
| viscosidad dinámica | pascal segundo | Pas | m1 kg s1 |
| momento de una fuerza | newton metro | Nm | m2kg s2 |
| tensión superficial | newton por metro | N/m | kgs2 |
| velocidad angular | radián por segundo | rad/s | mm1s1 = s1 |
| aceleración angular | radián por segundo cuadrado | rad/s2 | mm-1s2 = s2 |
| densidad superficial de flujo térmico, irradiancia | watt por metro cuadrado | W/m2 | kgs3 |
| capacidad térmica, entropía | joule por kelvin | J/K | m2kgs2K1 |
| capacidad térmica másica, entropía másica | joule por kilogramo - kelvin | J/(kgK) | m2s2K1 |
| energía másica | joule por kilogramo | J/kg | m2s2 |
| conductividad térmica | watt por metro - kelvin | W/(mK) | mkgs3K1 |
| densidad de energía | joule por metro cúbico | J/m3 | m1 kg s2 |
| campo eléctrico | volt por metro | V/m | m kg s3 A1 |
| densidad de carga eléctrica | coulomb por metro cúbico | C/m3 | m3 s A |
| densidad superficial de carga eléctrica | coulomb por metro cuadrado | C/m2 | m2 s A |
| densidad de flujo eléctrico, desplazamiento eléctrico | coulomb por metro cuadrado | C/m2 | m2 s A |
| permitividad | farad por metro | F/m | m3 kg1 s4 A2 |
| permeabilidad | henry por metro | H/m | m kg s2 A2 |
| energía molar | joule por mol | J/mol | m2 kg s2 mol1 |
| entropía molar, capacidad calorífica molar | joule por mol - kelvin | J/(molK) | m2 kg s2 K1 mol1 |
| exposición (rayos x, y ) | coulomb por kilogramo | C/kg | kg1 s A |
| tasa de dosis absorbida | gray por segundo | Gy/s | m2 s3 |
| intensidad radiante | watt por estereorradián | W/sr | m2 kg s3 |
| radiancia | watt por metro cuadrado- estereorradián | W/(m2sr) | kg s3 |
| concentración de actividad catalítica | katal por metro cúbico | kat/m3 | m3 s1 mol |
Los valores de distintas magnitudes pueden expresarse utilizando el mismo nombre y símbolo de unidad SI. De esta forma, por ejemplo, el joule por kelvin es el nombre de la unidad SI para la magnitud capacidad térmica, así como para la magnitud entropía. Debe indicarse tanto la unidad como la magnitud de medida. Esta regla debe aplicarse a los textos científicos, los textos técnicos, a instrumentos de medida, entre otros. Ver Capítulo 6.
Una unidad derivada puede expresarse de formas distintas utilizando unidades de base y unidades derivadas con nombres especiales: el joule, por ejemplo, puede escribirse newton metro o bien kilogramo metro cuadrado por segundo cuadrado. Esta libertad algebraica queda en todo caso limitada por consideraciones físicas de sentido común y, según las circunstancias, ciertas formas pueden resultar más útiles que otras.
En la práctica, para facilitar la distinción entre magnitudes diferentes que tienen la misma dimensión, se prefiere el uso de nombres especiales de unidades o combinaciones de nombres. Usando esta libertad, se pueden elegir expresiones que recuerden la definición de la magnitud. Como ejemplos, la magnitud momento de una fuerza puede considerarse como el resultado del producto vectorial de una fuerza por una distancia, lo que sugiere emplear la unidad newton metro; o la energía por unidad de ángulo aconseja emplear la unidad joule por radián. La unidad SI de frecuencia es el hertz que implica ciclos por segundo; la unidad SI de velocidad angular es el radián por segundo y la unidad SI de actividad es el becquerel, con el significado de cuentas por segundo. Aunque sería formalmente correcto escribir estas tres unidades como segundo a la potencia menos uno, el empleo de nombres diferentes sirve para subrayar las diferentes naturalezas de las magnitudes consideradas. El hecho de utilizar la unidad radián por segundo para expresar la velocidad angular y el hertz para la frecuencia, indica también que debe multiplicarse por 2 el valor numérico de la frecuencia en hertz para obtener el valor numérico de la velocidad angular correspondiente en radianes por segundo.
En el campo de las radiaciones ionizantes, la unidad SI de actividad es el becquerel en vez del segundo elevado a la potencia menos uno, y las unidades SI de dosis absorbida y dosis equivalente, respectivamente, son gray y sievert, en vez de joule por kilogramo. Los nombres especiales becquerel, gray y sievert se han introducido específicamente en atención a los peligros para la salud humana que podrían resultar en errores en el caso de que se empleasen las unidades segundo a la menos uno y joule por kilogramo para identificar a todas estas magnitudes.
5.2.3 Unidades para magnitudes adimensionales
Algunas magnitudes se definen como cocientes de dos magnitudes de la misma naturaleza por lo que su dimensión se expresa mediante el número uno, y son denominadas adimensionales o magnitudes de dimensión uno. La unidad SI coherente de todas las magnitudes adimensionales o magnitudes de dimensión uno, es el número uno, dado que esta unidad es el cociente de dos unidades SI idénticas. El valor de estas magnitudes se expresa por números puros y la unidad “uno” no se menciona explícitamente. Como ejemplos de tales magnitudes, se pueden citar el índice de refracción, la permeabilidad relativa o el coeficiente de fricción. Hay otras magnitudes definidas como un producto complejo y adimensional de magnitudes más simples. Por ejemplo, entre los “números característicos” cabe citar el número de Reynolds Re = rvl/h, en donde r es la densidad, h la viscosidad dinámica, v la velocidad y l una longitud. En todos estos casos, la unidad puede considerarse como el número uno, unidad derivada adimensional.
Otra clase de magnitudes adimensionales son los números que representan cuentas, como el número de moléculas, la degeneración de niveles de energía o la función de partición en termodinámica estadística correspondiente al número de estados termodinámicamente accesibles.
Para facilitar la identificación de la magnitud en cuestión, en algunos casos a esta unidad se le asigna un nombre especial como el radián o el estereorradián. El radián y el estereorradián reciben un nombre especial para la unidad derivada coherente uno, a fin de expresar los valores del ángulo plano y del ángulo sólido, respectivamente, y en consecuencia figuran en la Tabla 4.
NOTA 1: Para mayor información puede consultarse el Apéndice A.
5.2.4 Unidades no pertenecientes al SI aceptadas para su uso con unidades del SI
La Tabla 6 incluye las unidades no pertenecientes al SI cuyo uso con el Sistema Internacional se acepta dado que son ampliamente utilizadas en la vida cotidiana. Su utilización podría prolongarse indefinidamente; cada una de ellas tiene una definición exacta en unidades SI.
Tabla 6-Unidades no pertenecientes al SI cuyo uso con el SI se acepta.
| Magnitud | Nombre de la unidad | Símbolo de la unidad | Valor en unidades SI |
| tiempo | minuto | min | 1 min = 60 s |
| hora | h | 1 h = 60 min = 3600 s |
| día | d | 1 d = 24 h = 86 400 s |
| ángulo plano | grado (a) | ° | 1° = (/180) rad |
| minuto | ' | 1' = (1/60)° = (/10 800) rad |
| segundo | '' | 1' = (1/60)' = (/648 000) rad |
| área | hectárea | ha | 1 ha = 1 hm2 = 104 m2 |
| volumen | litro | L, l | 1 L = 1 l = 1 dm3 = 103 cm3 = 103 m3 |
| masa | tonelada | t | 1 t = 103 kg |
| (a) Se recomienda el uso de submúltiplos decimales del grado en lugar del minuto y el segundo; y del gon como otra unidad de ángulo plano. |
6. Prefijos para usarse con las unidades del SI y reglas de escritura
6.1 Prefijos para los nombres de múltiplos y submúltiplos
Los nombres y símbolos de prefijos para formar los nombres y símbolos de los múltiplos y submúltiplos decimales de las unidades SI desde 10-24 hasta 1024 son
Tabla 7-Prefijos del SI.
| Factor | Nombre | Símbolo |  | Factor | Nombre | Símbolo |
| 101 | deca | da |  | 10–1 | deci | d |
| 102 | hecto | h |  | 10–2 | centi | c |
| 103 | kilo | k |  | 10–3 | mili | m |
| 106 | mega | M |  | 10–6 | micro | µ |
| 109 | giga | G |  | 10–9 | nano | n |
| 1012 | tera | T |  | 10–12 | pico | p |
| 1015 | peta | P |  | 10–15 | femto | f |
| 1018 | exa | E |  | 10–18 | atto | a |
| 1021 | zetta | Z |  | 10–21 | zepto | z |
| 1024 | yotta | Y |  | 10–24 | yocto | y |
| Los prefijos SI representan estrictamente potencias de 10. No deben utilizarse para expresar potencias de 2 (por ejemplo, un kilobit representa 1 000 bits y no 1 024 bits). Los nombres y símbolos de los prefijos correspondientes a 210, 220, 230, 240, 250 y 260 son, respectivamente, kibi, Ki; mebi, Mi; gibi, Gi; tebi, Ti; pebi, Pi; y exbi, Ei. Así, por ejemplo, un kibibyte se escribe: 1 KiB = 210 B = 1 024 B, en donde B representa al byte. Aunque estos prefijos no pertenecen al SI, deben emplearse solamente en el campo de la tecnología de la información.
Estos prefijos, a excepción de algunas pocas unidades como el litro y el bar, no deben usarse para expresar unidades que no pertenecen al SI. Por ejemplo, no es válida la expresión “decigrados Celsius” ni el símbolo “d °C”. |
6.2 Signo decimal
El signo decimal debe ser una coma sobre la línea (,) o un punto sobre la línea (.).
Si la magnitud de un número es menor que la unidad, el signo decimal debe ser precedido por un cero. Cuando se use la coma como signo decimal, debe evitarse su uso para agrupar dígitos de tres en tres como es habitual en algunos ámbitos.
6.3 Reglas de escritura
6.3.1 Reglas de escritura para las Unidades
Los símbolos de las unidades deben ser escritos en caracteres del alfabeto romano –y no del alfabeto griego u otro-, rectos alineados con la vertical, independientemente del tipo de letra del texto adyacente. El símbolo de la unidad no debe pluralizarse, ni terminarse con un punto, excepto cuando se encuentre al final de un párrafo.
El signo de multiplicación para indicar el producto de dos o más unidades debe ser de preferencia un punto a media altura (·). Este punto puede suprimirse cuando la falta de separación de los símbolos de las unidades que intervengan en el producto no dé lugar a confusión.
Ejemplo: Nm o Nm, o también mN
pero no mN que se confunde con milinewton, submúltiplo de la unidad de fuerza.
Cuando una unidad derivada se forma por el cociente de dos unidades, dicho cociente puede expresarse utilizando una línea inclinada, una línea horizontal o bien potencias negativas.
Ejemplo: m/s o ms-1 para expresar la unidad de velocidad, metro por segundo
No se recomienda utilizar más de una línea inclinada en una sola expresión a menos que se agreguen paréntesis. En los casos complicados, deben utilizarse potencias negativas o paréntesis
Ejemplos: m/s2 o ms2, pero no: m/s/s
mkg/(s3A) o mkgs3A1, pero no: mkg/s3/A
No se permite usar los términos billón, trillón y sus respectivas abreviaciones.
No se admite usar las expresiones como partes en mil o partes por millón, especialmente al referirse a magnitudes relativas a contenidos, fraccioness. o concentraciones de sustancia.
6.3.2 Reglas de escritura para los prefijos
Los símbolos de los prefijos se escriben en caracteres del alfabeto romano –y no del alfabeto griego u otro-, rectos alineados con la vertical, de manera similar a los símbolos de las unidades, independientemente del tipo de letra del texto adyacente. Se unen a los símbolos de las unidades sin dejar espacio entre el símbolo del prefijo y el de la unidad. Con excepción de da (deca), h (hecto) y k (kilo), todos los símbolos de prefijos asociados con múltiplos se escriben con mayúsculas y todos los símbolos de prefijos asociados a submúltiplos se escriben con minúsculas. Todos los nombres de los prefijos se escriben con minúsculas, salvo cuando se encuentran al comienzo de una frase.
Ejemplos: pm (picómetro)
mmol (milimol)
GÙ (gigaohm)
THz (terahertz)
El grupo formado por un símbolo de prefijo y un símbolo de unidad constituye un nuevo símbolo de unidad, y por ello se torna inseparable (formando un múltiplo o un submúltiplo de la unidad que le dio origen). Puede ser elevado a una potencia positiva o negativa y puede combinarse con símbolos de otras unidades.
Ejemplos: 2.3 cm3 = 2.3 (cm)3 = 2.3 (102 m)3 = 2.3 × 106 m3
1 cm1 = 1 (cm)1 = 1 (102 m)1 = 102 m1 = 100 m1
1 V/cm = (1 V)/ (10–2 m) = 102 V/m = 100 V/m
5 000 µs1 = 5 000 (µs)1 = 5 000 (106 s)1 = 5 × 109 s1
Por lo mismo, los nombres de los prefijos son inseparables al escribir los nombres de las unidades a las que se unen. Así, por ejemplo, milímetro, micropascal y meganewton se escriben como una sola palabra, sin espacio u otro símbolo entre ellos.
No están permitidos los símbolos de prefijos compuestos; es decir, los símbolos de prefijos formados por yuxtaposición de dos o más símbolos de prefijos. Esta regla aplica también a los nombres de posibles prefijos compuestos.
Ejemplo: Es válido escribir nm (nanómetro), pero no lo es mµm (milimicrómetro).
Los símbolos de los prefijos no deben utilizarse solos o unidos al número 1, símbolo de la unidad uno. Igualmente, los nombres de los prefijos no deben unirse al nombre de la unidad uno, es decir a la palabra “uno”.
Ejemplo: El número de átomos de plomo en una muestra es igual a N(Pb) = 5 × 106, pero no N(Pb) = 5 M, en donde M representaría el prefijo mega.
6.3.3 El kilogramo
Por razones históricas, entre las unidades de base del Sistema Internacional la unidad de masa es la única cuyo nombre contiene un prefijo. Los nombres y los símbolos de los múltiplos y submúltiplos decimales de la unidad de masa se forman añadiendo los nombres de los prefijos a la palabra “gramo” y los símbolos de estos prefijos al símbolo de la unidad “g”.
NOTA 1: Es válida la expresión 10–6 kg = 1 mg, pero no 1 µkg (microkilogramo).
7. Vigilancia
La vigilancia del presente Proyecto de NOM estará a cargo de la Secretaría de Economía, por conducto de la Dirección General de Normas y de la Procuraduría Federal del Consumidor, conforme a sus respectivas atribuciones.
8. Concordancia con normas internacionales
Este Proyecto de Norma no es equivalente (NEQ) con ninguna Norma Internacional, por no existir esta última al momento de elaborar la Norma.
9. Bibliografía
- Ley Federal sobre Metrología y Normalización, publicada en el DOF el 1 de julio de 1992 y sus reformas.
- Reglamento de la Ley Federal sobre Metrología y Normalización , publicado en el DOF el 14 de enero de 1999 y sus reformas.
, publicado en el DOF el 14 de enero de 1999 y sus reformas.
- Le Système international d’unités SI 2006 publicado por la Oficina Internacional de Pesas y Medidas, BIPM, 2006.
- ISO 80000-1:2009, Quantities and units -- Part 1: General.
- ISO 80000-2:2009, Quantities and units -- Part 2: Mathematical signs and symbols to be used in the natural sciences and technology.
- ISO 80000-3:2006, Quantities and units -- Part 3: Space and time.
- ISO 80000-4:2006, Quantities and units -- Part 4: Mechanics.
- ISO 80000-5:2007, Quantities and units -- Part 5: Thermodynamics.
- IEC 80000-6:2008, Quantities and units -- Part 6: Electromagnetism.
- ISO 80000-7:2008, Quantities and units -- Part 7: Light.
- ISO 80000-8:2007, Quantities and units -- Part 8: Acoustics.
- ISO 80000-9:2009, Quantities and units -- Part 9: Physical chemistry and molecular physics.
- ISO 80000-10:2009, Quantities and units -- Part 10: Atomic and nuclear physics.
- ISO 80000-11:2008, Quantities and units -- Part 11: Characteristic numbers.
- ISO 80000-12:2009, Quantities and units -- Part 12: Solid state physics.
- IEC 80000-13:2008, Quantities and units -- Part 13: Information science and technology.
- IEC 80000-14:2008, Quantities and units -- Part 14: Telebiometrics related to human physiology.
- IERS Convention 2003 (D.D. McCarthy y G. Petit eds., IERS Technical Note 32, Frankfurt am Main: Verlag des Bundesamts für Kartographie und Geodäsie, 2004, 12).
- JPL ephemerides DE403 (Standish E.M., Report del IAU WGAS Sub-Group on Numerical Standards, Highlights of Astronomy, Appenzeller ed., Dordrecht: Kluwer Academic Publishers, 1995, 180-184).
- CODATA en 2002, publicada por P.J. Mohr y B.N. Taylor, Rev. Mod. Phys., 2005, 77, 1-107.
- NIST Special Publication 811 2008 Edition. Ambler Thompson and Barry N. Taylor. Guide for the. Use of the International. System of Units (SI).
Ciudad México, a 17 de diciembre de 2020.- El Director General de Normas y Presidente del Comité Consultivo Nacional de Normalización de la Secretaría de Economía, Lic. Alfonso Guati Rojo Sánchez.- Rúbrica.
NOTA:
Este Proyecto de NOM se publico el 4/III/2021 .
.